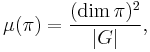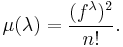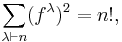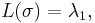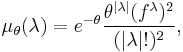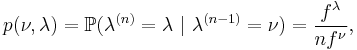Plancherel measure

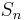In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group $G$ . In some cases the term Plancherel measure is applied specifically in the context of the group $G$ being the finite symmetric group $S_n$ – see below. It is named after the Swiss mathematician Michel Plancherel for his work in representation theory.

1 General definition
2 Definition on the symmetric group
3 Application
4 References

General definition

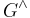Let $G$ be a finite group, we denote the set of its irreducible representations by $G^\wedge$ . The corresponding Plancherel measure over the set 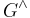$G^\wedge$ is defined by

$\mu(\pi) = \frac{(\mathrm{dim}\,\pi)^2}{|G|},$

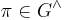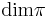where $\pi\in G^\wedge$ , and $\mathrm{dim}\pi$ denotes the dimension of the irreducible representation $\pi$ . ^[1]

Definition on the symmetric group 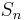$S_n$

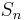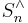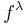An important special case is the case of the finite symmetric group $S_n$ , where $n$ is a positive integer. For this group, the set $S_n^\wedge$ of irreducible representations is in natural bijection with the set of integer partitions of $n$ . For an irreducible representation associated with an integer partition $\lambda$ , its dimension is known to be equal to $f^\lambda$ , the number of standard Young tableaux of shape $\lambda$ , so in this case Plancherel measure is often thought of as a measure on the set of integer partitions of given order n, given by

$\mu(\lambda) = \frac{(f^\lambda)^2}{n!}.$ ^[2]

The fact that those probabilities sum up to 1 follows from the combinatorial identity

$\sum_{\lambda \vdash n}(f^\lambda)^2 = n!,$

which corresponds to the bijective nature of the Robinson–Schensted correspondence.

Application

Plancherel measure appears naturally in combinatorial and probabilistic problems, especially in the study of longest increasing subsequence of a random permutation $\sigma$ . As a result of its importance in that area, in many current research papers the term Plancherel measure almost exclusively refers to the case of the symmetric group $S_n$ .

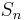Connection to longest increasing subsequence

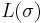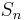Let $L(\sigma)$ denote the length of a longest increasing subsequence of a random permutation $\sigma$ in $S_n$ chosen according to the uniform distribution. Let $\lambda$ denote the shape of the corresponding Young tableaux related to $\sigma$ by the Robinson–Schensted correspondence. Then the following identity holds:

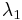$L(\sigma) = \lambda_1, \,$

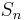where $\lambda_1$ denotes the length of the first row of $\lambda$ . Furthermore, from the fact that the Robinson–Schensted correspondence is bijective it follows that the distribution of $\lambda$ is exactly the Plancherel measure on $S_n$ . So, to understand the behavior of 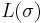$L(\sigma)$ , it is natural to look at 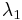$\lambda_1$ with $\lambda$ chosen according to the Plancherel measure in 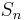$S_n$ , since these two random variables have the same probability distribution. ^[3]

Poissonized Plancherel measure

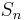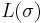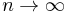Plancherel measure is defined on $S_n$ for each integer $n$ . In various studies of the asymptotic behavior of $L(\sigma)$ as $n \rightarrow \infty$ , it has proved useful ^[4] to extend the measure to a measure, called the Poissonized Plancherel measure, on the set 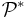$\mathcal{P}^*$ of all integer partitions. 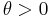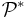For any $\theta > 0$ , the Poissonized Plancherel measure with parameter $\theta$ on the set $\mathcal{P}^*$ is defined by

$\mu_\theta(\lambda) = e^{-\theta}\frac{\theta^{|\lambda|}(f^\lambda)^2}{(|\lambda|!)^2},$

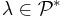for all $\lambda \in \mathcal{P}^*$ . ^[2]

Plancherel growth process

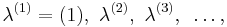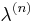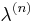The Plancherel growth process is a random sequence of Young diagrams $\lambda^{(1)} = (1),~\lambda^{(2)},~\lambda^{(3)},~\ldots,$ such that each $\lambda^{(n)}$ is a random Young diagram of order $n$ whose probability distribution is the nth Plancherel measure, and each successive $\lambda^{(n)}$ is obtained from its predecessor 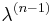$\lambda^{(n-1)}$ by the addition of a single box, according to the transition probability

$p(\nu, \lambda) = \mathbb{P}(\lambda^{(n)}=\lambda~|~\lambda^{(n-1)}=\nu) = \frac{f^{\lambda}}{nf^{\nu}},$

for any given Young diagrams $\nu$ and $\lambda$ of sizes n − 1 and n, respectively. ^[5]

So, the Plancherel growth process can be viewed as a natural coupling of the different Plancherel measures of all the symmetric groups, or alternatively as a random walk on Young's lattice. It is not difficult to show that the probability distribution of 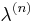$\lambda^{(n)}$ in this walk coincides with the Plancherel measure on 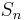$S_n$ . ^[6]

References

^ Borodin, A.; Okounkov, A. (2000). "Asymptotics of Plancherel measures for symmetric groups". J. Amer. Math. Soc.. 13:491–515.
^ ^a ^b Johansson, K. (2001). "Discrete orthogonal polynomial ensembles and the Plancherel measure". Ann. Math.. 153:259–296.
^ Logan, B. F.; Shepp, L. A. (1977). "A variational problem for random Young tableaux". Adv. Math.. 26:206–222.
^ Baik, J.; Deift, P.; Johansson, K. (1999). "On the distribution of the length of the longest increasing subsequence of random permutations". J. Amer. Math. Soc.. 12:1119–1178.
^ Vershik, A. M.; Kerov, S. V. (1985). "The asymptotics of maximal and typical dimensions irreducible representations of the symmetric group". Funct. Anal. Appl.. 19:21–31.
^ Kerov, S. (1996). "A differential model of growth of Young diagrams". Proceedings of St.Petersburg Mathematical Society.